Figure 1: The problem to solve

We have an underconstrained problem, which consists to put the tool point on the part edge (Figure 1).

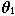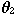• Let and denote the command valu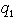es, and the actual joints' angles an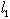d and the two links' lengths.
• Let 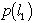be the prior information we have about length 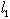precision (same for ) and 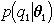the prior on the uncertainty we have on commanded joint value 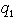(same for ).
• Let be the distance between the tool point and the part edge. will denote the distribution we expect on our objective variable .

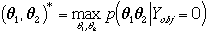
The Bayesian CAD module goes through the three following steps:

1. Using Bayesian formula, the symbolic module develops :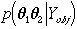

2. The summation module uses a Monte-Carlo simulation to compute integrals. The principle is to use the following approximation:

where is a probability density and is a large set of points drawn from .

3. The optimization module is used to obtain the command valuesthat maximize the objective function representing the problem.

We can see in the following figures two probability distributions using two different states of knowledge. We took in the two cases as a zero mean Gaussian distribution:

• In Figure 2, no uncertainties were assumed on links lengths and command values. All solutions that put the tool point on the edge have equal probabilities (appearing as the horizontal "crest" in the figure). It is the equivalent probabilistic solution to the analytical solution, which could be obtained by solving the equation .
  
  
• In Figure 3, we have assumed Gaussian distributions on links' lengths and command values. The propagation of uncertainties differs from one configuration to an other. Solutions are not equivalent because they correspond to different precision.

Figure 2: A map of the distribution over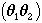 space assuming no uncertainty



Figure 3: A map of the distribution over 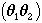space assuming
uncertainties on links lengths and command values