




IV.2.1. Vingt mille chiffres, pourquoi faire?
63440345364656151156061534064641465251521033623005046300322254412113052301311154450341430310354631163526145421006311535422106611063166501636113450363146622135544356655056156633461023164002653513524015542006163414234162151466054056114304121020040621104340024365001233563055332520664424344036536562115300256341211052520612500433532303211410664306553141442362131333232640664424630455324042133355351051640411136115401462155431151113600134435644261545425265165015154422605365451110625366344244502354325600641610264424222522250325122006030032516035231635603116503424140342452033211465410143516131015221520611226151255115160255035116014313110134136326456446662316134642225566625456240050622250342123341650143564606201602331432261116442210442110151305004631301133366620343112133301633663420155533353651143461404040621556666226454454534220115061432021334564053365454203055550632566132252626252360510532554663410445141114315151302333541130422060414605142631515532333416561534243125111325233216656113350115506605315161212160331005102240213152622333163256665302010510035201600630110243254216340645622432362234012402423430601412446213453265466355446213132434551045664622135515311453322363032161134351423331016502216631215063316011234015246655005523042134110312662156431454311526025320031012242132134056154306305135666464510605553313126146611051431631333445616210064350130361632260544236220361230043023066234112043646441335615424363116362246552434625165542346153544546463234022551546512013202205364441340440633526146331466500633225314465151403550145233154465436232145300262514300513024004442656605060304514304226656130240101550060112453332004212331603605363302421304150565354612620624430464054535104011230606566564344323341341510333501444423522104314056540422302245346063624025610622233566440031152654132201663536663114351151266202400621611414120401162163104506262662052303133641623025246251424620025350016001614343152451655321054511360362143563036414656400314114246633261451223163045360401602230254555150062433645410265021230063660161452140326162253030604565432442656005236455220212020264205340336635210106664462402022440252546061344016045661446313504163166300031653530044101514132232022012614103545556320220666565402261015061334622032211145411665012421506501603110010112330616644533554205510403003164422346251150654200501202211166015245504053432653260436044434000620461224204602516425061452262300506251561320201001411624010034022363351462436355230405114501050410603204441301332655453050105136203011453361064232461242553431165342054326141350016165301530565542232046342034331133163404030141334352114356531161242113142250361645206362031532165141564135106346146533542035156454501653451016335340566004630146643524615160420166226113163142352143164116646542130144021162302235446344030436415234052431534161115306226611315061061440555512064056306640421020104126016045544503615201013410000552232264015212401525620330351510146513223304551333513450564012356133546104020222264330230012101156201620434050006044154142606050116005042323356105120431630466445224644310156063426631500032510032266354335506456026626630131211120640030634036441202132130540264422210115432546223464525665232334426020603043252154563165605242425016365125525156641153412133024235560004104423204405555245633066611212265363033551331422125452464066404345551232334300525442242412311606311441205426341463133301132504135466165653422160503304004244516431060341562011506344315211041333355233643610645114066106020643035242632105621205323213035302134142150226345155161335141122103543206310622605401654364051566102610212416310156652163562606220034316351165356324620065321654520241503255500561530530246243153324261534133662664511164321156554344330006362623603012305435241430051120035466030010252356341360004054324002612654654463510455416330420432063616634402135256344465014553433602303513605044405062640410563112242406101016550254545445203035411646050062263043614511424046310355035015325132504350663406446620223125030513053131243533111606625453540645153355300302354013001161624402614630111502255605312600256553114133455016551616424240521244550655053036563260405303235510121336513602544266611646621446303113255644566064161235654201110304343435643263164556203202641444332200110502606034341334551305522636140066465523341405365521455403122112555314304032306340521101014425141203425512046032061422335263402440556612341101555162300600462231111324416546326664132130014606245126123010402234215020005242201556542304561461126265542363354135400042641246626515450356620404266633206200622632454552432433221211012365512416433140642065051116225055411105423531533116431113651301656641235113612221360153163535350341255216650514126624224452454661064233552336011055146130451120204324224401120366215533546224604445302466511432661366036526041651331425122044422113543661063645212103530134354111525662264103166044235226306522000526266365144230125560464243313060102514563216105423120433230155151614526020253502265052363626162651014265264261163035650133510444425430124146645150246611315145561356062545515536334460016364406400660666654402553146060510353422436025240431064440144556663656064100460366423135122231105630321460566100046045604501556360422114201236612324050410636111226642226626340224421533024413544045553041651430221513154145426534323310342645546011502653150504262523555212050604631422016225056401450021515564516554424542552332625001452520623042455463313035163353042633301054630504111145133360124133145634346022065045524344634511340331160001126222346314315616130411652212555423213123230031602651216462501553625253246601423441111251243232062011242404534346205005365022156604455234325311053164252026310425461133536120223315261332562030565062253102034515534041043454004520342345621121000343405334302020123510406456555505022501250444235232365422540263312035145114504510420205460324340336210536264321050236500041310264414216225616543056123245512336262052635321114000266002362213130144440413644441321021662540566142062021611046026010624015462052150561063662405505223446451403543443325366400531265066256000313563455055032353132513213110054606202622610514301031022005566442512441254332221364633136426040226311523562553522553533144514212200653051625214124022032011251325165263441561136666346660554345150654566401121030655120010531332641433305646126114463526541630166413532322505432512444064352066146230410266652353615303523354523436233456156566014156102442235552654121616461332211666361243225221151046366452563443103565426505623045550132554016642263101143466641156604464063005653253510224063310452425456134512234456334032503045121024303605233164313162510516030632203550665341005035612440326031614251220016260626012014220661443116400641515036546321342630365066325110166506006313052311445223502430045512320416655656645010333144440660666144146212336434202143363505126216553520545554130005425210221241305460223642064054121530501542645152401652433216125603321113266143216205100506205035600661066142620025501440435060135222511564543301152625252465525254543526241051441266030362302510623356663252314502201244516015611434610120411403443353610055536406215000415356203244603440455613562662624551513544655002626641550323642302542141503444302252414352023316003013244620231611146502566562130212143505550313422323360340006050105321351513034312224230053622634631036056616211021362045503055216052363401536334224026666560440550510554101066311003414204626052414024251410161623643222031036241024232505326134062153640112440102143605043230641051214310025150664620511433262622526435634122446535106265053466531152646566313335443121263203115346512010410446022542136562100450622152653046122522434553355200062433504133445026146025562105625304360301132132466466616412435333403104141603616240523511530062433153141435110135306106152034164231642251062102615332134625110600026300200053053144421610346525205404413310323263120446135306555202152010023455013006534312540502466213454426342204441303312620236412305651245624450346560563236265053405243020016110620163360331021001040630006146634251421631431562016463563242142631430651231446203021121643643402215120064400635155226004450322145004413504563016636140536436606304126530633241220423441540623630465044644662433433003616352610301543630253416554415665224205260225561246353404436325634541516036501156265035030562452400211661563515165510065526520361122654633231020426060161340345631344160456200056243550130161425526266252463153044143613103241455264110342430235151441433545055503345135252030563563040340205601301464303105564064106052322456335633111505254252225416616236041562523315353464600662132440564000250313500651220511554252535530403202136224646141234613152630011346322653203041245052331404342610325130143532550543560504202636465034352535652466616554602033012265200211556605400610132035515050316060104221005124653322034606312530133233263150256004530324233326213540106054061024010256324304622164026165010016540306206042540301661251341150551014020205204662004506541230030655644510145026445265230001060120104342521324030443452403356102650600352351221423014626442254111265454001163626424405205202310662120163206612115500605033024420350564550160314132264126430061033251041164536505063542161460045341115604320442650230636541101366355606650144643621561363634324353130335540530656064151115215366412450535356544531535136020101203424532060610453552566020221151465660354315146414266031610642400154302144430643615103155325532604111251244225224463225055521605352554565036625135044645242115002526311523250445230402450414166153550502344606406162304226254422145214323502333631664240524303363650144501156342205001630442126110660562360310554631121363246001422003523236213646416564050421336646315210242620022211153402031025254636326423515164445420414604330502303566120554151021634004331055666532604303150114140516001332146445416541224466634550430014460225506420013550531353366536231024562543164366300626322123224622020160262546211063663624261502624062613602603313005063625631063131153452360612261524355612064336664050230453333030320403624655146516142323023452354540450526105311623540423003405320564322353601261136656205034230633205515162251052552066212000414662162435253444425434146516115520143200154601304263542241034350253053660612665126305035032345116030421153625613215635156126103601042536645255401022035344300210554010143344444241634525134064423454211620346306544540345012052055026434266302404225550521644600546515032146325625314126666632433232406233461361331363004610422445064236320110115561054104363151630261651223162424501606000222141302150012622042052424424463562132544124666024203353524120663146515132532165315532503421455633543616544630563160150346020553022616540461654143043235145224031000335462542112303622332030143110035132201311135261446116054303661665222113163303450314340422545141652653545533325245652545012510546441030040461123141543634543112210636553512443513221163316041032551204200001113555305650534153055653504155352506061432622416001363055513336535324662410545360224511335053155251366141220560512231444315323063053412355216465123314411545454113463553146063052354050253352006340056526346400366525635435200052252322122161532040306214021621652134042304100620222315464663230333543011202536644346121323601610124401202543122544311464214223606332415363536201443661454065645566450602504241305232523001155315021532616212202205512644061306441425324630263243031420233362366552163551526326655230156300334005324612152325306606205302452114621114020535455030436623016232103422630120066043362130261031652101404434656554260234605543223021426202360441653543352442215214630122004100326056452116414511620235320611023426406502150301050324650423053443644034060653121436034206443464066562350621645361564534152544214502231356033102546116205164266460632322614540644562463145123346666351052126135221622524236151601060563013450222545156603143520032656426502201131324351031601144625331161663564434215411440115006532662024011355212425222022335240620463560222250501144050225245421523412514564406261003664016623643313234642304216345222055245613362512654612041032604254562043251303121664333124515440345315255132235414055252103154324263224556033361451235465521256620366556634551442421055260233001641461265521000441633360136044343265303305550454145331265400236150402624352600320056631644044113136613042114556534603005522101310232165620233366110003565266515525405011343451146640511255142235630504216342635304031422344123643111605545125450604454255610234016056020043301245335530441510252044200453146651205235662240252320110202003324404164632603124164246004246540432056110010152046331540042506306234203646606516411412235553545120015636026664041602626131625043050042154531645062303550102510051653006020225336250036455623423004551225324364664560032130243363540320040215114566206302521212202333433650155110526565326214151564411124220342662531415345155055132065406203126362604416405513602242162203266115005263021355616444206502625343361223241026054050211604353156516651462141113663156525432522360144113565254031511332140226051136653512640543253541323345233013053510453046662205634213506523321564036021635344443143221226464322541505343605304454616626124511152456414014021210135213506064021306200425106166212322654010113234500504565524555143305056141246345056024066422122631125033546606503510465525344150100434010415612213323165161461242435334430612111436534515651162515220650131154065530455500244165621442633021240121260626231650152424640253616464036511451360564264214555406330002115462561312622512646250332336631406334014215165431353143245426165104116250404455021053440321126334260132614312412533441424032350440043066246614352014212340513013162342210333641263461306556061352323204635053265443226305540561631244431104642332365031616511431263003204435463136036131146656525130246464606540552636106430033161564225563345125141012431035255301513101162150344623515221140651155522336511030013401036554351450635421335105431115104406005212313104516622501242212210002563231165125026641014445411012010312625503166463601432316205053666005461240451446561612623212523551055415545614322214421460026652200550302441532215135043222601616154353222666363620444355245601662161312105264530614235315420565415623561115052624220430356531144042024156245002553561425264611611252103625511453056346605431632420615131600454512345606402210126043354512002244044143425161100064445212134146500062444611102035663230055145110240510201005246323411405206032441044442216432103531053353433302440643215631664551416462353030256261461460350305163542406614454230535566611163264451333446230064012626206404321636455425561605555152431535444664640202155004231154563355015605441135432005112220253222062401345551250264130532361414113536221515244463136114066266214041622131234214260564561616511326633522142306164202216360532130113230132642035516606634226254356562253056043044541465626514305215125235423005544132001125305002243032066235463406135350510602000520153044364021524340024166511241153252551354535534444566623330444041130113345053144026450220460331211560256044056321426204601200106150342041355135612336035234056003250514131553363226065113111103630102133140352054643130515406046265550210240032112041001241363110502036661263434324445344023221422631145203016424526644130262355356130352361141236200333404350532524430265061406021006560113524231200004205540311402505044140544665140446362064365126235353341603241426633513341602602314415515123153562013400126662115560153166124266462351040132556450521262033631563106134112130561330114652613666305640235442011663012522212246652564115551353045060031114454063260054446455134631042115246502522250005331562516205024544331213445241632611341555462214426654655632031464262566153630230516462322441622422653540204222206215135010125043412561653305236065625052053236215526261150262050331045063036121224522332446354003441016505612432653033632306246141516662411115012160626120355242620033031426635034361144045650023063426451330660351034324425314661624545233213030435524325552520223402011403343224106320135462153641634500011442406460062364205661335046231563055054366014231603003402101300466226621662243045551330401156531661413305164406343135461604402422123015606622444152241466042364666215162036013240564063322516240120222554026622051456061662534512435646563551041536101514022330546353533521111203465205533645206611332543554363166606312624062512441306362614160436323136222600433655123045516111001266113260662561363115140451443660064635130454014133604134345221256541432134611435626434043543312113325641543201012063135631353353606005143202104362411225352640216414132242306303262656036116532105156010163105203133336015240406613125446164564213402203044265255162061350044030540650106004046156303060502065351125461560402203342612322343503304522460416464205464452212541110240535142350501636654354510610552052043222114506501653553243223216523345601513663613042042555656232360035655111346252141633163356232350515636413655423544524415033462311500330212315550030224264045200212154120420401032562545603045240426214452252455260334046542661461256356363162213531540053216152115133035350621046063444116212456144445111454436501264346615035445453404345125454166011053262464600040623254355425525114633614153033433563556002330211632202220545141615633254001024132420533024252306513650345523360665160655043523140326524023324343245001644241035643503153406356501106500114461402650336201040665111111124566164212321226542241134154664340242401251515652561635663132561233123224025412501452624656132462536322351323133524344456052022332231253206365212116010310640235554514004566142630461656652452256201133646145446104600505263445126234060532204335516162556254224410611363216112022134012634525030633606340504110362504203624503262520231253544104261530132244010156600362532263530263331446406363304150111201032351052265111354235304145521242155162624660064533000126136326666526364332463036533400254232164403333246422364206604041206423651026220020211302526641004200000111252645201365265455101005524352551146410141530002511212432236052504305542054013124463653035314452162333603504212616232223430013414630464561606506640015042451112043042354606511151433563443436050442154224446330163055624065306613110415504631503233511021203305162246110543221421060526651646500452044433502301422564003006551363462224100522241253023502015000124123465142266236042536553604121445615150424544441164040123225340623105250554506662136134101366500031456500460164203155320522150050365142652224501522545623120426330630342662611550565013162123332664453143612410146164401336524656120525210623606451241315520013205300216246312263223512332062140361425135203556452046232564551111321334661062353122313433652460513054412520112255264010151003662621652365016453654406353254460443451630533260163560253002624204555135226155523510303324062363640233061254201001456543203664261265514526453005246665656462423020322066622232013120566544120365531150130335602244342131022030125110361423510063115520031225153620624202435025636465234033311206351311653556165355015455324261501500401655034536454100424511126502261110055246633314325233506663033313351013526440134010241135030130324031623323232506263453161532460161413305166212100120456033512025033050334245310555426050434662550651316214531405244363566120364224411201062540633003056140615342032346230120002232146540144462664440150502551500355010251055102546105262144665105052111256643140221204022132513430433404202255405514601542231213600423263415462006031532115010421100566563623542510240455335635036440354243552660322516622613023634061524510523025161643416356535516323403203265065644313140504365156146451663413065203440532231635114661361531121545256131224336122431322000152025533460156160240312422541311615221406306244620131102413110355423143064111052510045032461631363264525123534163615443156155410425313465236420155634231133463061261214025146524213065445531152413312264006264212552356633151612164464253452006320343012262562604221652020614661016563406115310255160223010250023654542544335523416141526626046124052035341213613650105124055511630165633350642453005643003522466403032532011002410624500062602126226421253261261441503602216461216313345155266040631065615532
Figure 16 : 20 000 chiffres, pourquoi faire?
Exemple extrêmement réduit de jeux de données expérimentales.
Les capteurs du Khépéra transmettent une telle quantité
d'informations toutes les 10 secondes.
Une caméra vidéo en transmet 2 500 fois plus chaque seconde.
Supposons que nous ayons à notre disposition un ensemble de données
expérimentales brutes sous la forme de 20 000 chiffres (voir figure
16). Un tel jeu de données est manifestement inexploitable tel quel.
Sans connaissances préalables, ce n'est qu'une suite de signes cabalistiques
sans aucune espèce de signification possible.
Une connaissance préalable minimale absolument requise consiste à
préciser comment ces 20 000 chiffres se repartissent pour former
des nombres. Supposons qu'ici chaque chiffre soit un nombre. On a donc pas
20 000 chiffres mais 20 000 nombres correspondant à 20 000 valeurs
de n variables.
Une deuxième connaissance préalable nécessaire est
de garantir que ces 20 000 données forment un tout cohérent,
correspondant bien à l'observation d'un seul et même phénomène
et qu'il convient bien d'essayer de les analyser ensemble. [21]
Une troisième connaissance préalable consiste à préciser
le nombre n de variables et à répartir les 20 000 valeurs
sur les n variables. Supposons qu'ici une seule variable V ait été
observée. Nous avons donc 20 000 expériences concernant V.
Enfin, une quatrième connaissance préalable tout à
fait déterminante suppose que l'ordre (temporel et/ou spatial) dans
lequel ces 20 000 expériences se présentent n'est pas pertinent.[22]
Par ces choix, nous avons défini l'espace des phases et placé
les points expérimentaux. Les connaissances préalables de
ce type ont été qualifiées de structurelles au paragraphe
III.
Un premier travail sur les données devient maintenant possible. On
peut en construire l'histogramme en dénombrant pour chaque valeur
observée de la variable le nombre de fois ou elle est apparue (voir
la ligne ni du tableau 1). Un histogramme n'est pas une distribution de
probabilité (et donc pas une description) mais il permet une réduction,
éventuellement considérable, de l'information.
Pour pouvoir produire notre première description il faut encore faire
une hypothèse supplémentaire, à savoir le nombre de
valeurs possibles que peut prendre la variable observée. On peut
alors démontrer ([Jayne95]) que la meilleure description possible
est la loi de succession de Laplace :
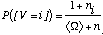 [4.12]
[4.12]
avec <[Omega]> le nombre de valeurs possibles pour V, ni
le nombre d'expériences où la valeur i a été
mesurée et n le nombre d'expériences totales.
Cette loi de succession de Laplace ce rapproche de l'histogramme dès
que le nombre d'expériences n devient grand devant le nombre de cas
possible <[Omega]>.
Elle présente, cependant, deux avantages sur l'histogramme : elle
se comporte bien quand le nombre d'expériences n est faible (notamment,
on retrouve la distribution uniforme pour n=ni=0) et, surtout,
elle ne fixe la probabilité d'aucun événement à
0, évitant par là, un choix définitif devant reposer
sur une certitude (une probabilité de 0 ne peut pas évoluer
par apprentissage et rend impossible tout événement dépendant
de l'événement de probabilité nulle).
Cette loi de succession de Laplace est la forme la plus rudimentaire de
description de données expérimentales. Celle qui suppose le
moins de connaissances préalables et, donc, "colle" au
plus près les données. Celle, aussi qui nécessite le
plus de paramètres étant donné que pour coder n données
il faut <[Omega]> paramètres.
Supposons que nous apprenions maintenant que la variable V peut prendre
une quelconque des 6 valeurs entre 1 et 6 (<[Omega]>=6). Nous allons
alors pouvoir calculer effectivement les probabilités pour chaque
valeur de V (voir ligne L du tableau 1). Notre collection de données
expérimentales commence à "prendre du sens" et à
permettre le raisonnement. Il devient notamment possible de faire des prédictions
sur les résultats à venir.
La loi de succession de Laplace s'avère rapidement complètement
inadaptée dès que l'on a des connaissances préalables
plus riches. De ce fait, elle a souvent été critiquée
dans l'histoire des probabilités.
Par exemple, la loi de succession de Laplace attribue une probabilité
de 11/12 à un enfant de dix ans de vivre une année de plus
(<[Omega]>=2, ni=10, n=10) alors qu'elle attribue pour
son grand-père de 70 ans une probabilité de 71/72 au même
événement (<[Omega]>=2, ni=70, n=70). Ce
résultat nous choque par son inexactitude évidente. Cependant,
ce n'est pas la loi de succession de Laplace qui est en cause, c'est simplement
que pour juger de la validité de ce résultat, nous disposons
d'informations préalables qui n'ont pas été prises
en compte pour établir ces probabilités.
Curieusement, face à des problèmes de ce genre, de nombreux
auteurs ont jugé que les calculs utilisant la loi de succession de
Laplace devaient être faux, ou ont invoqué d'obscurs principes
pour bannir l'utilisation de cette distribution, alors qu'ils leur suffisaient
de constater que son emploi n'était tout simplement pas en accord
avec leurs prémisses.
Mathématiquement, rechercher la distribution maximisant H revient
à résoudre un problème d'optimisation sous contraintes.
Bien qu'en théorie le principe de maximum d'entropie soit applicable
à n'importe quel type de connaissances préalables, il s'avère
qu'en pratique, il est la plupart du temps insoluble analytiquement.
Il existe, cependant, un type de contraintes (connaissances préalables)
génériques et très souvent rencontré dans la
pratique (notamment en physique) pour lequel on connaît la forme analytique
de la distribution de maximum d'entropie solution. Il s'agit du cas où
les connaissances préalables C sont données sous forme de
m fonctions réelles fj, nommées observables,
et pour lesquelles on peut calculer leurs moyennes Fj sur les
données expérimentales. On assume alors que les descriptions
adéquates du phénomène sont données par les
distributions P pour lesquelles les espérances des fonctions fj
sont égales aux moyennes expérimentales Fj.
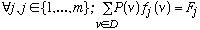 [4.13]
[4.13]
La distribution de maximum d'entropie correspondant à ces contraintes
est alors P* donnée par :
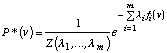 [4.14]
[4.14]
avec, Z la fonction de partition, donnée par :
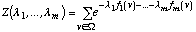 [4.15]
[4.15]
les m [lambda]i pouvant être déterminés par
les m équations traduisant les contraintes [4.13]:
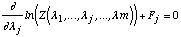 [4.16]
[4.16]
Ce type de distributions "exponentielles" permet de coder n données
avec m paramètres qui sont au choix, soit les Fi appelés
"niveaux de contraintes" des observables, soit les [lambda]i
appelés "multiplicateurs de Lagrange".
Il existe en physique un très grand nombre de telles distributions
de maximum d'entropie correspondant au choix de tel ou tel ensemble d'observables,
à commencer, bien sûr, par les distributions habituelles de
la physique statistique.
La plus connue de ces distributions de maximum d'entropie exponentielle
est la Gaussienne. Elle correspond au cas à une variable V, avec
les 2 observables f1(V)=V et f2(V)=V2.
La Gaussienne est donc la distribution de maximum d'entropie lorsque ce
que l'on a retenu des expériences c'est leur moyenne expérimentale
et celle de leur carré.
Appliquons ce type de raisonnement à nos 20 000 expériences.
Supposons que nous apprenions que nos 20 000 expériences sont les
résultats de lancers consécutifs d'un dé. Force est
de constater d'après les résultats expérimentaux que
ce dé semble largement pipé (la loi de succession de Laplace
obtenue est très différente de la distribution uniforme escomptée).
Un dé est un cube dans lequel de légères excavations
ont été faites pour graver les chiffres sur les faces. Chacune
de ces excavations provoque un léger déplacement du centre
de gravité du dé en direction opposée. Une première
hypothèse possible (C1) pour justifier le biais constaté consiste
alors à dire que globalement le centre de gravité se déplace
de manière à favoriser l'apparition des faces les plus légères,
c'est-à-dire celles portant les chiffres les plus élevés.
Pour tenter d'observer cet effet escompté, nous choisissons l'observable
f1(V)=. La moyenne expérimentale de f1(V)=
vaut F1=3,5983. L'application du principe de maximum d'entropie nous conduit
alors à une description du phénomène (une distribution
de maximum d'entropie) ayant la forme :
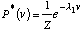 [4.17]
[4.17]
avec 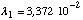 et Z une constante de normalisation. Les probabilités
correspondantes sont données dans la ligne C1 du tableau 2.
et Z une constante de normalisation. Les probabilités
correspondantes sont données dans la ligne C1 du tableau 2.
Ces valeurs semblent encore très mal rendre compte des expériences.
Il est possible d'usiner 5 faces d'un dé sans avoir à le manipuler.
Par contre, l'usinage de la dernière face suppose obligatoirement
une manipulation et donc une perte de précision. On peut donc supposer
qu'un dé a de bonne chance d'avoir un coté légèrement
plus long (ou plus court) que les 2 autres. L'apparition des deux faces
correspondantes sera alors légèrement moins probable (ou plus
probable) que celle des 4 autres. On a donc 3 nouvelles hypothèses
à tester :
- - le coté reliant les faces 1 et 6 est de longueur différente
(C2)
- - le coté reliant les faces 2 et 5 est de longueur différente
(C3)
- - le coté reliant les faces 3 et 4 est de longueur différente
(C4)
Prenons l'exemple de l'hypothèse C2, on peut essayer d'en quantifier
l'observation avec l'observable f2(V)=0 si V vaut 2, 3, 4 ou
5 et f2(V)=-1 si V vaut 1 ou 6. La moyenne expérimentale
de f2(V) vaut donc :
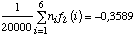 [4.18]
[4.18]
L'application du principe de maximum d'entropie à cette hypothèse
C2, nous conduit alors à une description du phénomène
(une distribution de maximum d'entropie) ayant la forme:
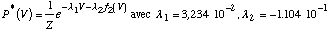 [4.19]
[4.19]
Les probabilités correspondantes sont données dans la ligne
C2 du tableau 1. Les mêmes calculs peuvent être effectués
pour les hypothèses C3 et C4. Les résultats correspondants
sont présentés dans le tableau 1 aux lignes C3 et C4.
|
V=1 |
V=2 |
V=3 |
V=4 |
V=5 |
V=6 |
Total |
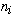 |
3246 |
3449 |
2897 |
2841 |
3635 |
3932 |
20000 |
U
Uniforme |
0.16666 |
0.16667 |
0.16667 |
0.16667 |
0.16666 |
0.16667 |
1 |
L
Laplace |
0,16230 |
0,17245 |
0,14486 |
0,14206 |
0,18174 |
0,19659 |
1 |
| C1 |
0,15294 |
0,15818 |
0,16361 |
0,16922 |
0,17502 |
0,18103 |
1 |
| C2 |
0,16497 |
0,15259 |
0,15760 |
0,16278 |
0,16813 |
0,19393 |
1 |
| C3 |
0,14803 |
0,16808 |
0,15843 |
0,16390 |
0,18612 |
0,17543 |
1 |
| C4 |
0,16433 |
0,16963 |
0,14117 |
0,14573 |
0,18656 |
0,19258 |
1 |
Tableau 1
A la vue du tableau 1 l'hypothèse C4 semble rendre compte des
données expérimentales beaucoup mieux que les autres. Cette
intuition peut se vérifier mathématiquement en appliquant
les techniques déjà rencontrées précédemment
sous le nom de "problème inverse". La règle [R1]
nous donne:
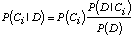 [4.20]
[4.20]
Si nous supposons, a priori, que les 6 hypothèses en présence
(U, L, C1, C2, C3 et C4) sont équiprobables, nous obtenons:
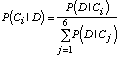 [4.21]
[4.21]
P(D|Ci) est donné par :
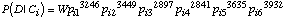 [4.22]
[4.22]
W (indépendant de Ci) est le nombre de permutations sur les 20000
expériences avec 3246 fois le résultat 1, 3449 fois le résultat
2, 2897 fois le résultat 3, 2841 fois le résultat 4, 3635
fois le résultat 5 et 3932 fois le résultat 6. Pij
est la probabilité d'obtenir le résultat j pour l'hypothèse
Ci.
En effectuant les calculs numériques on obtient :
Hypothèses |
Laplace |
C4 |
C2 |
C3 |
C1 |
U |
| P(Ci | D) |
0.99 |
0.01 |
10-32 |
10-35 |
10-45 |
10-59 |
Tableau 2
L'hypothèse C4 est donc énormément plus probable
que toutes les autres (sauf Laplace).
L'hypothèse C4 ayant une interprétation et une justification
physique, on est libre de considérer qu'il vaut mieux l'adopter comme
description que Laplace[23]. C'est
un choix subjectif, qui peut se traduire mathématiquement en lui
donnant une probabilité a priori P(C4) beaucoup plus grande que P(L),
celle de la description loi de succession de Laplace.
En fait, les données utilisées dans cet exemple sont des données
réelles issues d'une expérience menée par Wolf il y
a plus d'un siècle.
Six nombres (les nombres de fois où chacun des 6 résultats
possibles est apparu), quelques connaissances préalables traduisant
un peu de bon sens physique et le principe de maximum d'entropie, nous permettent
de penser avec une très grande confiance que ce dé que nous
n'avons, bien évidemment, jamais vu, était légèrement
oblong suivant l'axe "3-4".
[21]Cette exigence peut parraître
évidente et triviale, pourtant les physiciens et les biologistes
savent bien l'extrème difficultée qu'il peut y avoir à
garantir l'intégrité d'un jeu de données vis-à-vis
d'un phénomène observé.
Le choix des données à traiter ensemble est, en fait, fondamental
car il défini implicitement le phénomène qu'on veut
étudier.
Si, par exemple, on sépare le jeu de 20 000 données en 2 cela
signifie qu'on supose qu'une variable "cachée" (non mesurée)
a changée d'état et qu'on préfére étudier
ce qu'on a observé comme 2 phénomènes séparés.
C'est aussi souvent à ce stade que certaines données sont
écartées car jugées "abhérentes".
En rejetant ces données comme "extérieur" au phénomène,
on lui définit subjectivement des limites.
[22]Ce choix est très "compromettant",
car il suppose que les dépendances existant entre ces 20 000 valeurs
ne sont d'origine ni spatiale ni temporelle.
[23]Ce genre de connaissances préalables
ayant un sens physique conduit par exemple, en général, a
de bien meilleure généralisation que la loi de succession
de Laplace.
D'autre part, elles présentent l'immense avantage pratique de conduire
a des représentations becoup plus compacte que la loi de succession
de Laplace. m (nombre d'observables) paramètres sont suffisants,
au lieu des <[Omega]> nécessaires avec Laplace.





[4.12]
[4.13]
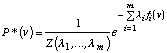
[4.15]
[4.16]
[4.17]
et Z une constante de normalisation. Les probabilités
correspondantes sont données dans la ligne C1 du tableau 2.
[4.18]
[4.19]
[4.20]
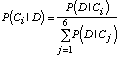
[4.22]