Pour une description donnée, on peut distinguer les deux ensembles de variables ou de propositions suivants :
Soit D un ensemble de mesures des variables de [Delta] appelé
ensemble de données, soit C un ensemble de valeurs pour les variables
de [Chi] appelé ensembles de paramètres ou connaissances préalables,
on s'intéresse à l'étude des probabilités conjointes
de D et C.
La règle [R1] nous donne :
P(DC) = P(C) x P(D|C) = P(D) x P(C|D)
Si l'on admet connaître les valeurs de certains paramètres
et si l'on fixe par hypothèse celles des autres, le "problème
direct" consiste à "prédire" les valeurs des
données. Mathématiquement, cela signifie que l'on cherche
P(D|C).
Inversement, si l'on connaît un ensemble de données et que
l'on cherche P(C|D) on traite le "problème inverse". Il
consiste à chercher les paramètres qui rendent "au mieux"
compte des expériences ou encore à choisir parmi plusieurs
hypothèses envisageables laquelle est la plus probable. On voit qu'en
particulier, le problème inverse recouvre les problèmes de
type identification dont il a été question au paragraphe précédent.
Pour illustrer le problème direct et le problème inverse et
pour donner quelques exemples élémentaires de raisonnement
probabiliste, plaçons-nous dans le cas ou notre système est
une urne de Bernouilli remplie de boules blanches et noires dans laquelle
on effectue des tirages sans remise.
La connaissance préalable C s'exprime par les propositions N = "L'urne
contient n boules" et par B "L'urne contient b boules blanches",
paramétrées par n et b.
Les données D peuvent s'exprimer, par exemple, sous la forme Ti
= "On observe le tirage d'une boule blanche au ième
tirage".
Nous allons, pour le problème direct, nous intéressé
aux probabilités de D, c'est-à-dire de Ti, sachant
C, c'est-à-dire n et b.
Intéressons-nous, tout d'abord à la probabilité P(T2
|C) de tirer une boule blanche au deuxième tirage. Nous pouvons écrire
que T2 = (T1 + ~T1)T2 = T1T2
+ ~T1T2. En appliquant la règle [R3] puis la
règle [R1] on obtient :
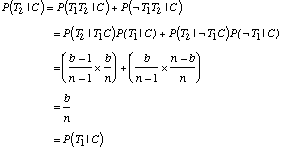
Ce qui nous montre que la probabilité d'avoir une boule blanche au
deuxième tirage (ne sachant pas le résultat du premier) est
la même que celle d'avoir une boule blanche au premier tirage. Il
en est d'ailleurs de même pour tous les tirages.
Intéressons-nous maintenant à P(T1|2C)
la probabilité de tirer une boule blanche au premier tirage sachant
le tirage d'une boule blanche au deuxième.
La règle [R1] nous donne :
[4.4]
Comme on vient de démontrer en [4.3] que :
On obtient:
[4.5]
Ce raisonnement peut se reproduire pour un i et un j quelconque et on obtient
finalement :
[4.6]
Ce résultat peut étonner à plus d'un titre. En particulier,
car il peut paraître surprenant que la probabilité du tirage
d'une boule blanche au premier tirage puisse être influencée
par le deuxième tirage. Une idée très profondément
ancrée dans nos esprits cartésiens et newtoniens est qu'un
événement ne peut être influencé que par les
événements qui l'ont précédé dans le
temps. En fait, ce résultat, contrairement aux apparences, ne remet
pas en cause ce principe de la physique. La confusion vient de ce que l'on
considère que le premier tirage a été influencé
par le second alors que ce que nous dit le résultat [4.5] c'est que
la connaissance que l'on a de ce qui peut se passer au premier tirage est
éventuellement influencée par la connaissance du résultat
du deuxième tirage. Il faut bien distinguer entre la causalité
physique qui ne peut que se propager vers le futur et la capacité
d'inférence logique qui fonctionne aussi bien dans un sens que dans
l'autre.
Le calcul qui a conduit à [4.5] est particulièrement simple
et résulte d'un usage tout à fait élémentaire
des règles des probabilités. Pourtant, même ce résultat
trivial n'est compréhensible que si l'on considère une distribution
de probabilité comme l'état de connaissance d'un individu
sur un certain phénomène et non pas comme une description
de ce phénomène indépendamment de l'observateur. Ce
seul exemple pose déjà un sérieux problème pour
toute épistémologie objectiviste des probabilités.
Plaçons-nous maintenant, pour illustrer le problème inverse,
dans le cas où n le nombre total de boules est connu mais où
b le nombre de boules blanches n'est pas connu. On va chercher à
cerner b grâce à un ensemble de données D constitué
avec des tirages issus de cette urne.
Alors que pour le problème direct, nous nous intéressions
à la probabilité de D sachant C=NB, nous nous intéressons,
maintenant à la probabilité de B sachant D et N, d'où
le nom de problème inverse.
La règle [R1] nous donne :
P(BD|N) = P(B|N) x P(D|BN) = P(D|N) x P(B|DN) [4.7]
d'où on tire :
[4.8]
Nous constatons que le résultat recherché dépend, d'une
part, de P(D|BN) la probabilité directe et, d'autre part, de P(B|N)[20] appelé distribution "a
priori" qui doit être soit donnée soit calculable pour
que l'on puisse effectuer le calcul. P(D|N) n'est pas à considérer,
car elle peut toujours être obtenue par normalisation en sommant P(B|DN)
sur toutes les valeurs de B possibles.
Il apparaît donc, une nouvelle fois, que le résultat d'une
série d'expériences (D) n'est pas interprétable en
soi, mais uniquement au jour de connaissances préalables apportées
ici par la distribution a priori. Voici un deuxième exemple de ce
qui vient juste d'être dit, à savoir que le raisonnement probabiliste
ne peut pas être la description d'une quelconque réalité
indépendante de l'observateur, mais nécessite pour interpréter
toute donnée la présence d'informations préalables
sur l'état de connaissance de cet observateur.
Il serait trop long de développer ici les calculs pour les différentes
distributions a priori envisageables. Nous invitons donc le lecteur à
se reporter au chapitre 6 de [Jaynes95] pour satisfaire sa curiosité
concernant P(B|DN).