III.3.1. Utilisation et apprentissage de comportements réactifs

Dans cette première série d'expériences, nous avons cherché à doter Khépéra de comportements purement réactifs vis-à-vis des obstacles. Les commandes motrices sont directement inférées des valeurs sensorielles.

Prenons l'exemple de l'évitement d'obstacle. Le but poursuivi est de donner la capacité à Khépéra d'éviter les obstacles et d'aller en ligne droite lorsqu'il est en espace libre.

Nous avons choisi d'utiliser pour cette expérience les 3 variables Dir, Prox et Vrot. La description correspondante va donc être une distribution de la forme :

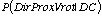[3.5]

Le protocole expérimental adopté est constitué de 2 phases:

• Une phase d'apprentissage pendant laquelle Khépéra est piloté par un opérateur à l'aide d'un joystick. Durant cette phase les données expérimentales D (valeurs des variables sensorielles Dir et Prox et de la commande motrice Vrot) sont enregistrées et les paramètres, permettant de stocker P(Dir Prox Vrot | D C) en machine, sont identifiés
• Une phase de restitution où Khépéra évite les obstacles tout seul. Les calculs formels probabilistes sont alors utilisés pour calculer à chaque instant la commande motrice Vrot à envoyer aux roues en fonction des données sensorielles Dir et Prox provenant des capteurs de proximité.

La description P(Dir Prox Vrot | D C) obtenue lors de l'apprentissage, dépend évidemment des expériences D, mais aussi, et d'une certaine manière surtout, des connaissances préalables C.
Les connaissances préalables C données par le concepteur peuvent être regroupées en 4 catégories de natures différentes :

• les connaissances préalables structurelles sont définies par l'ensemble des variables {V₁,...,V_n} sur lesquelles la distribution de probabilité va être construites. Pour notre exemple, comme il a déjà été dit, 3 variables ont été choisies : Dir, Prox et Vrot.
• Les connaissances préalables de dépendances sont données par une structure de dépendance[11] permettant de décomposer de manière unique une description comme un produit de distributions plus simples. Ces simplifications essentielles sont fondées sur des considérations d'indépendances conditionnelles entre variables. Pour l'exemple qui nous occupe, les règles des probabilités donnent :

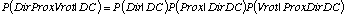[3.6]

• Nous pensons a priori qu'il n'existe pas de corrélations particulières entre la direction dans laquelle on observe un obstacle et la distance à cet obstacle. Nous traduisons cette connaissance pour notre robot en lui disant que Prox est indépendante de Dir conditionnellement à D et C.

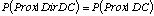[3.7]

• On obtient donc :

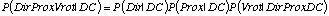[3.8]

• Les connaissances a priori donnent des valeurs initiales (avant apprentissage) aux distributions ou explicitent une méthode pour les calculer à partir d'autres distributions connues. Une connaissance a priori peut aussi, par exemple, exprimer qu'une distribution est supposée ne pas évoluer en fonction des données.
• Nous n'avons aucune raison de penser que le robot sera amené à rencontrer les obstacles suivant une direction privilégiée ou à une distance particulière. Nous adoptons donc comme a priori que toutes les couples (Dir, Prox) sont équiprobables, ce qui se traduit par :

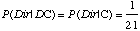[3.9]

• et par :

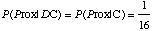[3.10]

• Enfin, les connaissances préalables d'observation, qui se décomposent en la spécification d'une représentation paramétrique et d'un processus d'apprentissage (identification des paramètres) pour chacune des distributions de la structure de dépendances. Une représentation paramétrique permet d'une part, de représenter ces distributions en machine et d'autre part, d'identifier leurs paramètres par apprentissage.
• Pour cette expérience, on a utilisé une loi de succession de Laplace comme représentation paramétrique de :

[3.11]

• Où :
  • m_dp est le nombre de fois où la situation sensorielle Dir=d et Prox=p a été rencontrée pendant l'apprentissage
  • m_v est le nombre de fois ou Vrot=v a été observé pour la situation sensorielle précédente.
  • 21 est le nombre de valeurs possibles pour Vrot.
• Pour un nombre important d'expériences, la loi de succession de Laplace se rapproche d'un simple histogramme défini par m_v/m_dp. Les termes correctifs 1 et 21 servent à traiter les cas où le nombre d'expériences est faible. En particulier pour m_v=m_dp=0, on trouve 1/21 soit la distribution uniforme.

Par le calcul formel, on peut alors, en phase de restitution commander Khépéra en choisissant à chaque instant Vrot suivant la distribution P(Vrot |Dir Prox D C).
La commande de Khépéra par cette méthode fonctionne très bien. Après un temps d'apprentissage de quelques minutes, (< 5 minutes) on obtient le comportement souhaité (voir figure 11). Le comportement obtenu s'avère être très "robuste" au changement de position, de taille, de forme, de matière, de couleurs[12] et même de vitesse des obstacles, ainsi qu'aux conditions d'éclairage de la scène.

Figure 11 : comportement d'évitement d'obstacle

Avec la même méthode et les mêmes connaissances préalables, en changeant l'apprentissage téléopéré au "joystick", on a appris a Khépéra à suivre les murs et contours (voir figure 12) et à poursuivre les obstacles mobiles.

Figure 12 : comportement de suivi de contour

Avec la même méthode, sur la base des variables Vrot et Lum nous avons appris à Khépéra un comportement photophile représenté par la description P(Vrot Lum | D' C').